Stationary sequence
In probability theory – specifically in the theory of stochastic processes, a stationary sequence is a random sequence whose joint probability distribution is invariant over time. If a random sequence X j is stationary then the following holds:
where F is the joint cumulative distribution function of the random variables in the subscript.
If a sequence is stationary then it is wide-sense stationary.
If a sequence is stationary then it has a constant mean (which may not be finite):
See also
References
- Probability and Random Processes with Application to Signal Processing: Third Edition by Henry Stark and John W. Woods. Prentice-Hall, 2002.
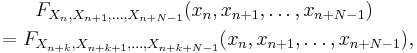
![E(X[n]) = \mu \quad \text{for all } n .](/2012-wikipedia_en_all_nopic_01_2012/I/aba10d2df6c5e3521bd871552ce204f9.png)